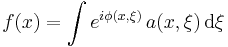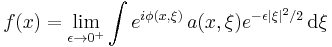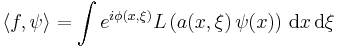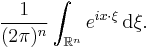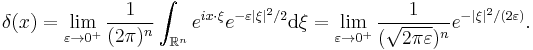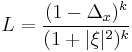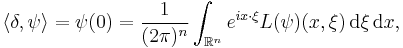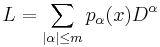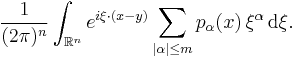Oscillatory integral

In mathematical analysis an oscillatory integral is a type of distribution. Oscillatory integrals make rigorous many arguments that, on a naive level, appear to use divergent integrals. It is possible to represent approximate solution operators for many differential equations as oscillatory integrals.

Contents

Definition

An oscillatory integral f(x) is written formally as

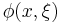f(x) = \int e^{i \phi(x,\xi)}\, a(x,\xi) \, \mathrm{d} \xi

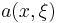where \phi(x,\xi) and a(x,\xi) are functions defined on 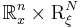\mathbb{R}_x^n \times \mathrm{R}^N_\xi with the following properties.

1) The function \phi is real valued, positive homogeneous of degree 1, and infinitely differentiable away from \{\xi = 0 \} . Also, we assume that \phi does not have any critical points on the support of a . Such a function, \phi is usually called a phase function. In some contexts more general functions are considered, and still referred to as phase functions.
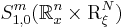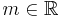2) The function a belongs to one of the symbol classes S^m_{1,0}(\mathbb{R}_x^n \times \mathrm{R}^N_\xi) for some m \in \mathbb{R}. Intuitively, these symbol classes generalize the notion of positively homogeneous functions of degree m . As with the phase function \phi , in some cases the function a is taken to be in more general, or just different, classes.

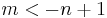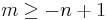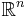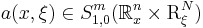When m < -n %2B 1 the formal integral defining f(x) converges for all x and there is no need for any further discussion of the definition of f(x) . However, when m \geq - n%2B1 the oscillatory integral is still defined as a distribution on \mathbb{R}^n even though the integral may not converge. In this case the distribution f(x) is defined by using the fact that a(x,\xi) \in S^m_{1,0}(\mathbb{R}_x^n \times \mathrm{R}^N_\xi) may be approximated by functions that have exponential decay in \xi. One possible way to do this is by setting

f(x) = \lim \limits_{\epsilon \rightarrow 0^%2B} \int e^{i \phi(x,\xi)}\, a(x,\xi) e^{-\epsilon |\xi|^2/2} \, \mathrm{d} \xi

where the limit is taken in the sense of tempered distributions. Using integration by parts it is possible to show that this limit is well defined, and that there exists a differential operator L such that the resulting distribution f(x) acting on any \psi in the Schwarz space is given by

\langle f, \psi \rangle = \int e^{i \phi(x,\xi)} L \left ( a(x,\xi) \, \psi(x) \right ) \, \mathrm{d} x \, \mathrm{d} \xi

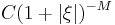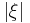where this integral converges absolutely. The operator L is not uniquely defined, but can be chosen in such a way that depends only on the phase function \phi , the order m of the symbol a , and N. In fact, given any integer M it is possible to find an operator L so that the integrand above is bounded by C (1 %2B |\xi|)^{-M} for |\xi| sufficiently large. This is the main purpose of the definition of the symbol classes.

Examples

Many familiar distributions can be written as oscillatory integrals.

1) The Fourier inversion theorem implies that the delta function, 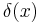\delta(x) is equal to
\frac{1}{(2 \pi)^n} \int_{\mathbb{R}^n} e^{i x \cdot \xi} \, \mathrm{d} \xi.
If we apply the first method of defining this oscillatory integral from above, as well as the Fourier transform of the Gaussian, we obtain a well known sequence of functions which approximate the delta function:
\delta(x) = \lim_{\varepsilon \rightarrow 0^%2B}\frac{1}{(2 \pi)^n} \int_{\mathbb{R}^n} e^{i x\cdot \xi} e^{-\varepsilon |\xi|^2/2} \mathrm{d} \xi = \lim_{\varepsilon \rightarrow 0^%2B} \frac{1}{(\sqrt{2 \pi \varepsilon})^n} e^{-|\xi|^2/(2 \varepsilon)}.
An operator L in this case is given for example by
L = \frac{(1 - \Delta_x)^k}{(1 %2B |\xi|^2)^k}
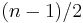where \Delta_x is the Laplacian with respect to the x variables, and k is any integer greater than (n-1)/2. Indeed, with this L we have
\langle \delta, \psi \rangle = \psi(0) = \frac{1}{(2 \pi)^n}\int_{\mathbb{R}^n} e^{i x \cdot \xi} L(\psi)(x,\xi)\, \mathrm{d} \xi \, \mathrm{d} x,
and this integral converges absolutely.
2) The Schwartz kernel of any differential operator can be written as an oscillatory integral. Indeed if
L = \sum \limits_{|\alpha| \leq m} p_\alpha(x) D^\alpha
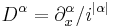where D^\alpha = \partial^\alpha_{x}/i^{|\alpha|} , then the kernel of L is given by
\frac{1}{(2\pi)^n}\int_{\mathbb{R}^n} e^{i \xi \cdot (x - y)} \sum \limits_{|\alpha| \leq m} p_\alpha(x) \, \xi^\alpha \, \mathrm{d} \xi.

Relation to Lagrangian distributions

Any Lagrangian distribution can be represented locally by oscillatory integrals (see Hörmander (1983)). Conversely any oscillatory integral is a Lagrangian distribution. This gives a precise description of the types of distributions which may be represented as oscillatory integrals.

See also

References